Leicht kompliziertes mathematisches Rätsel
Vor ein paar Tagen bin ich über dieses Rätsel von Heinrich Hemme gestolpert.
Die Frage lautet, wie man diese Figur in drei deckungsgleiche Teile zerlegen kann.
Die im Artikel genannte Lösung ist irgendwie kompliziert. Vor allem ignoriert sie die gelben Kästchen. In der Lösung heißt es: "Wenn man sich nicht durch das quadratische Raster irritieren lässt, ist die Aufgabe ganz einfach."
Guckt euch die Lösung im Artikel an und sagt mir, warum das so kompliziert gemacht wurde. Ich meine – drei deckungsgleiche Teile. Das hätte jeder Tetris-Spieler sofort hinbekommen ohne da komplizierte Schnitte quer durch die Figur machen zu müssen.
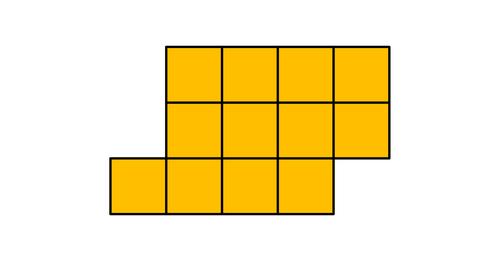
Die Frage lautet, wie man diese Figur in drei deckungsgleiche Teile zerlegen kann.
Die im Artikel genannte Lösung ist irgendwie kompliziert. Vor allem ignoriert sie die gelben Kästchen. In der Lösung heißt es: "Wenn man sich nicht durch das quadratische Raster irritieren lässt, ist die Aufgabe ganz einfach."
Guckt euch die Lösung im Artikel an und sagt mir, warum das so kompliziert gemacht wurde. Ich meine – drei deckungsgleiche Teile. Das hätte jeder Tetris-Spieler sofort hinbekommen ohne da komplizierte Schnitte quer durch die Figur machen zu müssen.
Trackbacks
Keine Trackbacks
Kommentare
Ansicht der Kommentare: Linear | Verschachtelt
Mathegenie am :
Nicht der Andere am :
Nicht der Andere am :
Panther am :